Integrating surfaces and solids of revolution with ���wheels���
P(p) is the parameter range of P.
![]()
Sliders to set roots of polynomial f(p):
![]()
![]()
![]()
![]()
![]()
Scaling factor for polynomial f(p):
![]()
f(p) is the function to be revolved around axis.
![]()
![]()
Area of sector (of a circle) of angle a :
![]()
Area of an annular (flat ring) sector with outer radius r , innner radius s, and angle a:
![]()
Volume of a disk-sector of radius r, angle a, and thickness T:
![]()
Volume of the sector of a wheel of square cross-section with outer radius r , innner radius s, angle a, and thickness T :
![]()
The edges of a rectangle with left at l, bottom at b, width w and height h.
p is the drawing parameter.
![function(E,1,l,b,w,h,p)=vector(l+w*p,b,0),function(E,2,l,b,w,h,p)=vector(l+w,b+h*p,0),function(E,3,l,b,w,h,p)=vector(l+w*[1-p],b+h,0),function(E,4,l,b,w,h,p)=vector(l,b+h*[1-p],0)](formula23.png)
Filling in the interior of the rectangle:
u is the horizontal and v is the vertical parameter.
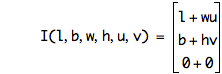
Plots
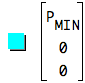
Dots at minimum and maximum x-values:
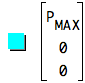
Plot the curve on the xy plane:
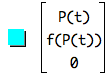
Rotation around the x-axis by the angle a:
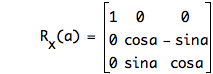
Rotate the curve:
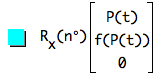
The interiors of the rectangles, at start and rotated:
function(I,K*W,0,W,(K*W)^2,u,v),in(k,set(4,5,6,7,8,9,10))
function(R_x,n*degree)*function(I,K*W,0,W,(K*W)^2,u,v),in(k,set(4,5,6,7,8,9,10))
The width of the wheels:
![]()
The edges of the rectangles, at start:
![]()
![]()
![]()
![]()
The edges of the rectangles, rotated:
![]()
![]()
![]()
![]()
The surfaces swept out by the edges:
![]()
![]()
![]()
![]()
This file was created by Graphing Calculator 3.5.
Visit Pacific Tech to download the helper application to view and edit these equations live.